Answer:
56.641 feet
Explanation:
Use the equation
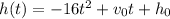 to find the vertical distance of an object travelling at a speed of
to find the vertical distance of an object travelling at a speed of
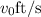 at initial height
at initial height
 after
after
 seconds.
seconds.
First, we find the time at which the ball will reach maximum height:
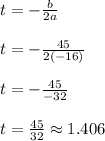
Second, we find the vertical distance of the ball after
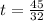 seconds:
seconds:

Therefore, the golf ball will reach a maximum height of 56.641 feet after 1.406 seconds.