Question

If vector A has components Ax and Ay and makes an angle θ with the +x axis, thena. Ax +Ay (where A is magnitude of A)b. θ= Ay/Axc. Cosθ= Ax/ √ (Ax^2+ Ay^2)d. Tanθ= Ax/Ay

Answer 1

c. Cos θ =
`A_(x)` /
`\sqrt{(A_(x) ^(2) + A_(y) ^(2)) }`

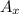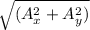
Step-by-step explanation:

A vector is any quantity that has both magnitude and direction. The given vector A has components
`A_(x)` and
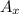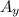`A_(y)`, and makes angle θ with +x axis.

Thus;

Resultant of the vector, A =
`\sqrt{(A_(x) ^(2) + A_(y) ^(2)) }`

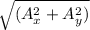
Therefore, the components, angle and resultant of vector A can be represented in magnitude and direction by the three sides of a right angled triangle.

Applying the appropriate trigonometric function to the triangle for vector A, we have;

Cos θ =
`A_(x)` ÷
`\sqrt{(A_(x) ^(2) + A_(y) ^(2)) }`

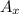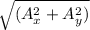
⇒ Cos θ =
`A_(x)` /
`\sqrt{(A_(x) ^(2) + A_(y) ^(2)) }`

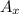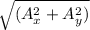
The correct option is C.