Question

A reaction in which A, B, and C react to form products is zero order in A, one-half order in B, and second order in C.

a. Write a rate Jaw for the reaction.

b. What is the overall order of the reaction?

c. By what factor does the reaction rate change if [A] is doubled (and the other reactant concentrations are held constant )?

d. By what factor does the reaction rate change if [B] is doub led (and the other reactant co ncen trati ons are held consta nt )?

e. By what factor does the reaction rate change if [C] is doubled (and the other reactant concen trations are held constant)?

f. By what factor does the reaction rate change if the concentrations of all three reactants are doubled?

Answer 1

a.
`r=k[B]^(1/2)[C]^2`

b.
`Order=3.5`

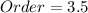
c. It does not affect the rate.

d.
`√(2)`.

e. 4.

f. 4
`√(2)`.

Step-by-step explanation:

Hello,

In this case, considering the given information, we have:

a.
`r=k[B]^(1/2)[C]^2`

b. By adding 1/2 and 2 (powers for B and C), the overall order is:

`Order=(1)/(2) +2\\\\Order=3.5`

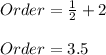
c. It is not changed, since the concentration of A is not affecting the rate due to its specific zeroth-order.

d. In this case, if the concentration of B is doubled, such term in the equation shows:

`\sqrt[n]{x} (r_f)/(r_i)=([2B]^((1/2)) [C]^2)/([B]^((1/2))[C]^2) \\\\(r_f)/(r_i)=([2B]^((1/2)))/([B]^((1/2)))\\\\(r_f)/(r_i)=((2)/(1))^(1/2)\\\\r_f=√(2) r_i`

It means that the rate increases by a factor of
`√(2)`.

e. In this case, if the concentration of C is doubled, such term in the equation shows:

`(r_f)/(r_i)=([B]^((1/2))[2C]^2)/([B]^((1/2))[C]^2) \\\\(r_f)/(r_i)=(([2C])/([C]))^(2)\\\\(r_f)/(r_i)=((2)/(1))^(2)\\\\r_f=4r_i`

It means that the rate increases by a factor of 4.

f. In this case, if the concentration of both B and C are doubled, such terms in the equation shows:

`(r_f)/(r_i)=([2B]^((1/2))[2C]^2)/([B]^((1/2))[C]^2) \\\\(r_f)/(r_i)=(2^((1/2))2^2)/(1^((1/2))1^2) \\\\(r_f)/(r_i)=4√(2) \\\\r_f=4√(2) r_i`

It means that the rate increases by a factor of 4
`√(2)`.

Best regards.