Question

Find the value of y if B is between A and C, AB is 2y, BC is 6y, and AC is 48.

Answer 1

7. C. 6

8. H. √34

9. A. (1, 3.5)

10. J. 10

Explanation:

7. AB = 2y, BC = 6y, AC = 48

AB + BC = AC (segment addition theorem)

Substitute the above values into the equation

2y + 6y = 48

Solve for y

8y = 48

Divide both sides by 8

8y/8 = 48/8

y = 6

8. Distance between P(2, 8) and Q(5, 3):

`PQ = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

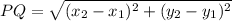
Let,

`P(2, 8) = (x_1, y_1)`

`Q(5, 3) = (x_2, y_2)`

`PQ = √((5 - 2)^2 + (3 - 8)^2)`

`PQ = √((3)^2 + (-5)^2)`

`PQ = √(9 + 25)`

`PQ = √(34)`

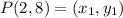
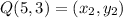
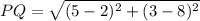
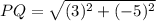
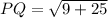
9. Midpoint (M) of segment LB, for L(8, 5) and B(-6, 2) is given as:

`M((x_1 + x_2)/(2), (y_1 + y_2)/(2))`

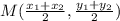
Let
`L(8, 5) = (x_1, y_1)`

`B(-6, 2) = (x_2, y_2)`

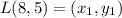
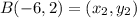
Thus:

`M((8 + (-6))/(2), (5 + 2)/(2))`

`M((2)/(2), (7)/(2))`

`M(1, 3.5)`

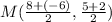
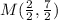
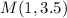
10. M = -10, N = -20

Distance between M and N, MN = |-20 - (-10)|

= |-20 + 10| = |-10|

MN = 10