Question

What is the solution of the system of equations? y = –2x + 8 y = x – 4

Answer 1

(4,0)

Explanation:

So we have the system of equations:

`y=-2x+8\\y=x-4`

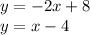
To solve, we can use substitution.

Substitute the second equation into the first. So:

`x-4=-2x+8`

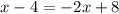
Add 2x to both sides. The right cancels:

`3x-4=8`

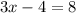
Add 4 to both sides:

`3x=12`

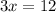
Divide both sides by 3:

`x=4`

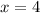
Now, let's substitute this back into the second equation to find y:

`y=x-4`

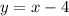
Substitute 4 for x:

`y=4-4`

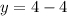
Subtract:

`y=0`

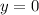
So, our solution is (4,0).

And we're done!