Question

Given the points A(-2,-1) and B(-6,5), find the value of the y-coordinate of point C which is 23 from point A to point B.

Answer 1

Given:

Points A(-2,-1) and B(-6,5).

Point C which is 2/3 from point A to point B.

To find:

The y-coordinate of point C.

Solution:

Let the coordinates of point C are (a,b).

Point C which is 2/3 from point A to point B.

AC:AB = 2:3

AC:CB = AC:(AB-AC) = 2:(3-2) = 2:1

Section formula: If a point divides the line segment in m:n, then then

`Point=\left((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\right)`

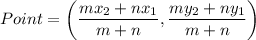
Point C divides AB in 2:1, soby section formula

`C=\left((2(-6)+1(-2))/(2+1),(2(5)+1(-1))/(2+1)\right)`

`C=\left((-12-2)/(3),(10-1)/(3)\right)`

`C=\left((-14)/(3),(9)/(3)\right)`

`C=\left((-14)/(3),3\right)`

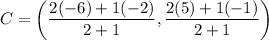
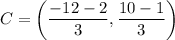
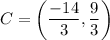
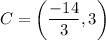
Therefore, the y-coordinated of point C is 3.