Question

Find the center and radius of this

circle:
(x – 7)2+(y + 4)2= 49
Center = ([ ? 1,1])
Radius = [

Answer 1

Center = (7, -4)

Radius = 7

Explanation:

The general equation of a circle is:

`(x-h)^(2)+(y-k)^(2)=r^(2)`

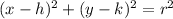
where (h, k) is the center of the circle and r is the radius.

The equation given is in the form of the general equation of a circle. Knowing this, we will be able to find the center and radius by finding h, k, and r.

`(x-7)^(2)+(y+4)^(2)=49`

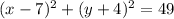
We can turn the 49 into 7² (√49 = 7, so 49 = 7²) and turn the equation into:

`(x-7)^(2)+(y+4)^(2)=7^(2)`

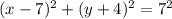
Now we can see that:

h = 7

k = -4

r = 7

So the center of the circle would be (7, -4) and the radius would be 7.

I hope you find my answer helpful.

Answer 2

`\text{Hello there! :)}`

Answer:

`\boxed{\text{Center at } (7, -4), \text{ Radius of } 7.}`

`\text{Formula for a circle: } (x - h)^(2) + (y - k)^(2) = r^(2) \text{ Where:}`

`h = \text{ x-coordinate of center}\\\\k = \text{ y-coordinate of center}\\\\r = \text{ radius}\\\\\text{Therefore:}`

`\text{In the equation } (x - 7)^(2) + (y + 4)^(2) = 49:`

`h = 7\\\\k = -4\\\\r = \sqrt[]{49} = 7 \\\\\text{So:}`

`\text{Center at } (7, -4), \text{ Radius of } 7.`