Answer:
The answer is
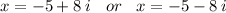
Explanation:
x² + 10x + 89 = 0
Using the quadratic formula
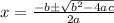
From the question
a = 1 , b = 10 , c = 89
Substitute the values into the above formula and solve
We have
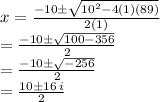
Separate the real and imaginary part
That's
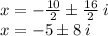
We have the final answer as
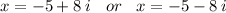
Hope this helps you