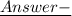
the given figure is a composition of a rectangle as well as a right angled triangle !
we've been given the two sides of the rectangle and we're required to find out the height of the triangle , so as to find it's area ~
we know the the opposite sides of a rectangle are equal , therefore we can break the longest side ( length = 9.5 cm ) into two parts ! the first part of length = 7 cm which is the length of the rectangle and the rest 2.5 cm ( 9.5 - 7 = 2.5 ) will become the height of the triangle !
For perimeter of the figure -
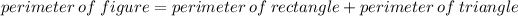
now ,
perimeter of rectangle = 2 ( l + b )
where ,
l = length
b = breadth
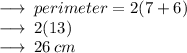
and ,

Perimeter of figure in total = 26 cm + 15 cm
thus ,
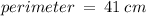
For area of the figure -

now ,
area of rectangle = l × b
where ,
l = length
b = breadth

and ,
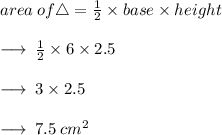
Area of figure in total = 42 cm² + 7.5 cm²
thus ,
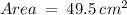
hope helpful :)