Answer:
All real numbers ( -∞ ,∞)
Explanation:
Simplify
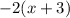
Apply the distributive property.
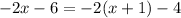
Simplify
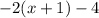
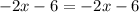
Move all terms containing x to the left side of the equation.
Add 2 x to both sides of the equation.
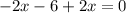
Combine the opposite terms in
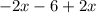
add
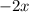 and
and
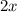
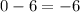
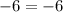
Since
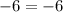 , the equation will always be true for any value of x . All real numbers
, the equation will always be true for any value of x . All real numbers
The result can be shown in multiple forms.
All real numbers
Interval Notation:
( − ∞ , ∞ )