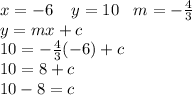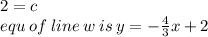Question

Line v passes through point (6,6) and is perpendicular to the graph of y =3/4x-11. Line w is parallel to line v and passes through point (-6, 10).

Which is the equation of line w in slope-intercept form?

Answer 1

`y = - (4)/(3) x + 2`

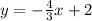
Explanation:

It was stated that Line V which passes through the point (6 , 6) and is perpendicular to the graph of

`y = (3)/(4) x - 11`

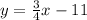
Since line V is perpendicular to this graph it means that line V's gradient is the negative inverse of this graphs' gradient. The gradient of the graph is

`(3)/(4)`

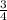
Hence the gradient of line v is: (let the gradient of line v be x)

`(3)/(4)x = - 1 \\ x = ( - 1)/( (3)/(4) ) \\ x = - 1 * (4)/(3) \\ x = - (4)/(3)`

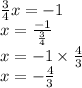
Therefore the gradient of line V is - 4/3. Since line W is parallel to line V, it would have the same gradient which is -4/3. The question also stated that line W passes through the point (-6 , 10). Therefore

`x = - 6 \: \: \: \: \: y = 10 \: \: \: \: m = - (4)/(3) \\ y = mx + c \\ 10 = - (4)/(3) ( - 6) + c \\ 10 = 8 + c \\ 10 - 8 = c`

`2 = c \\ equ \: of \: line \: w \: is \: y = - (4)/(3) x + 2`