Question

The corners of a meadow are shown on a coordinate grid. Ethan wants to fence the meadow. What length of fencing is required?

On the grid: Point A (-6,2); Point B (2,6); Point C (7,1); Point D (3,-5)

Answer 1

34.6 units

Explanation:

The lenght of fencing required is the total distance between point A to B, B to C, C to D, and D to A. That is the distance between all 4 corners of the meadow.

The coordinates of the corners of the meadow is shown on a coordinate plane in the attachment. (See attachment below).

Let's use the distance formula to calculate the distance between the 4 corners of the meadow using their coordinates as follows:

Distance between point A(-6, 2) and point B(2, 6):

`AB = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

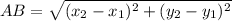
Let,

`A(-6, 2)) = (x_1, y_1)`

`B(2, 6) = (x_2, y_2)`

`AB = √((2 - (-6))^2 + (6 - 2)^2)`

`AB = √((8)^2 + (4)^2)`

`AB = √(64 + 16) = √(80)`

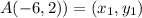
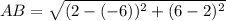
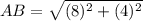
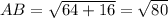
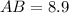`AB = 8.9` (nearest tenth)

Distance between B(2, 6) and C(7, 1):

`BC = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

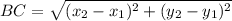
Let,

`B(2, 6) = (x_1, y_1)`

`C(7, 1) = (x_2, y_2)`

`BC = √((7 - 2)^2 + (1 - 6)^2)`

`BC = √((5)^2 + (-5)^2)`

`BC = √(25 + 25) = √(50)`

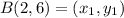
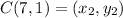
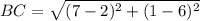
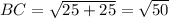
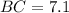`BC = 7.1` (nearest tenth)

Distance between C(7, 1) and D(3, -5):

`CD = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

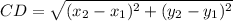
Let,

`C(7, 1) = (x_1, y_1)`

`D(3, -5) = (x_2, y_2)`

`CD = √((3 - 7)^2 + (-5 - 1)^2)`

`CD = √((-4)^2 + (-6)^2)`

`CD = √(16 + 36) = √(52)`

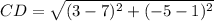
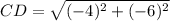
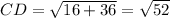
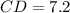`CD = 7.2` (nearest tenth)

Distance between D(3, -5) and A(-6, 2):

`DA = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

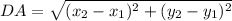
Let,

`D(3, -5) = (x_1, y_1)`

`A(-6, 2) = (x_2, y_2)`

`DA = √((-6 - 3)^2 + (2 - (-5))^2)`

`DA = √((-9)^2 + (7)^2)`

`DA = √(81 + 49) = √(130)`

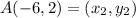
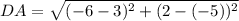
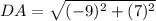
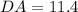`DA = 11.4` (nearest tenth)

Length of fencing required = 8.9 + 7.1 + 7.2 + 11.4 = 34.6 units