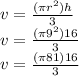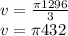Answer:
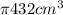
Explanation:
The formula to calculate the volume of a cone is
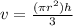
Since they asked that we determine the volume in terms of pi, we are not going to equate pi to its numerical value.

I am not sure if the radius is 9 cm because the image is kinda blurry. If it is not 9 cm you can input the actual radius into the formula to find the volume.