Question

What are the minimum and maximum values of x, for which x3 + x2 – 6x ≥ 0? minimum = –3, maximum = 0 minimum = 0, maximum = 2 minimum = –3, no maximum minimum = 2, no maximum Please answer quickly

Answer 1

minimum = –3, no maximum

Explanation:

The other guy here was completely correct, but just in case it assures anyone's doubts:

Answer 2

Answer: Option C.

Explanation:

The given inequality is

`x^3+x^2-6x\geq 0`

Taking x common, we get

`x(x^2+x-6)\geq 0`

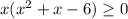
Splitting the middle term, we get

`x(x^2+3x-2x-6)\geq 0`

`x(x(x+3)-2(x+3))\geq 0`

`x(x+3)(x-2)\geq 0`

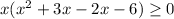
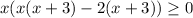
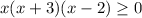
Related equation is

`x(x+3)(x-2)=0`

`x=-3,0,2`

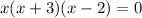
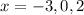
These three points divide the number line in 4 parts.

Interval Sign of
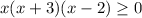`x(x+3)(x-2)\geq 0` Statement

(-∞,-3)
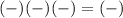`(-)(-)(-)=(-)` False

(-3,0)
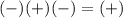`(-)(+)(-)=(+)` True

(0,2)
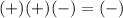`(+)(+)(-)=(-)` False

(2,∞)
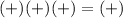`(+)(+)(+)=(+)` True

So, the solution set is (-3,0) ∪ (2,∞).

Thus, minimum value is –3 and no maximum value.

Therefore, the correct option is C.