Answer: Option C.
Explanation:
The given inequality is
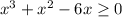
Taking x common, we get
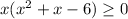
Splitting the middle term, we get
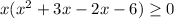
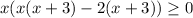
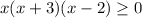
Related equation is
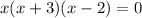
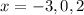
These three points divide the number line in 4 parts.
Interval Sign of
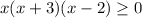 Statement
Statement
(-∞,-3)
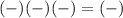 False
False
(-3,0)
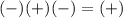 True
True
(0,2)
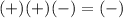 False
False
(2,∞)
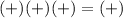 True
True
So, the solution set is (-3,0) ∪ (2,∞).
Thus, minimum value is –3 and no maximum value.
Therefore, the correct option is C.