Question

A 1.00 kg sample of water at 9.00°C is in a calorimeter. You drop a piece of steel with a mass of 0.370 kg at 210°C into it. After the sizzling subsides, what is the final equilibrium temperature (in °C)? (Make the reasonable assumptions that any steam produced condenses into liquid water during the process of equilibration and that the evaporation and condensation don't affect the outcome.)

Answer 1

The final temperature of the water-steel system is 16.853 ºC.

Step-by-step explanation:

We consider the system of water sample and the piece of steel as control mass, which is supposed to be an isolated system, that is, a system with no mass and energy transfer with surroundings. As water has more mass and a higher specific heat that piece of steel, it is very unlikely that evaporation and condensation would affect the outcome.

The piece of steel is cooled down while water is heated up, until thermal equilibium is reached. By First Law of Thermodynamics, we must observe that:

`Q_(water)-Q_(steel) = 0`

`Q_(water) = Q_(steel)`

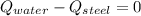
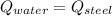
Where:

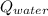`Q_(water)` - Heat received by the water sample, measured in joules.

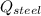`Q_(steel)` - Heat released by the piece of steel, measured in joules.

Now, we expand each term by definition of sensible heat:

`m_(w)\cdot c_(w)\cdot (T-T_(w,o))=m_(s)\cdot c_(s)\cdot (T_(s,o)-T)`

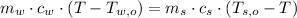
Where:

`m_(w)`,
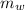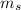`m_(s)` - Masses of the water sample and the piece of steel, measured in kilograms.

`c_(w)`,
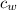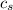`c_(s)` - Specific heat of water and steel, measured in joules per kilogram-Celsius.

`T_(w,o)`,
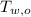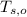`T_(s,o)` - Initial temperatures of the water sample and the piece of steel, measured in Celsius.

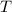`T` - Final temperature of the sample-piece system, measured in Celsius.

The final temperature is cleared:

`(m_(w)\cdot c_(w)+m_(s)\cdot c_(s))\cdot T = m_(w)\cdot c_(w)\cdot T_(w,o)+m_(s)\cdot c_(s)\cdot T_(s,o)`

`T = (m_(w)\cdot c_(w)\cdot T_(w,o)+m_(s)\cdot c_(s)\cdot T_(s,o))/(m_(w)\cdot c_(w)+m_(s)\cdot c_(s))`

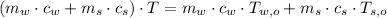
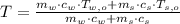
If we know that
`m_(w) = 1\,kg`,
`m_(s) = 0.370\,kg`,
`c_(w) = 4186\,(J)/(kg\cdot ^(\circ)C)`,
`c_(s) = 460\,(J)/(kg\cdot ^(\circ)C)`,
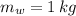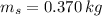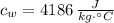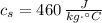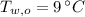`T_(w,o) = 9\,^(\circ)C` and
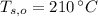`T_(s,o) = 210\,^(\circ)C`, the final temperature of the system is:

`T = ((1\,kg)\cdot \left(4186\,(J)/(kg\cdot ^(\circ)C) \right)\cdot (9\,^(\circ)C)+(0.370\,kg)\cdot \left(460\,(J)/(kg\cdot ^(\circ)C) \right)\cdot (210\,^(\circ)C))/((1\,kg)\cdot \left(4186\,(J)/(kg\cdot ^(\circ)C) \right)+(0.370\,kg)\cdot \left(460\,(J)/(kg\cdot ^(\circ)C) \right))`

`T = 16.853\,^(\circ)C`

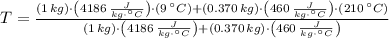
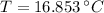
The final temperature of the water-steel system is 16.853 ºC.