Question

An object thrown in the air has a velocity after t seconds that can be described by v(t) = -9.8t + 24 (in meters/second) and a height h(t) = -4.9t 2 + 24t + 60 (in meters). The object has mass m = 2 kilograms. The kinetic energy of the object is given by K = __1 2mv2 , and the potential energy is given by U = 9.8mh. Find an expression for the total kinetic and potential energy K + U as a function of time. What does this expression tell you about the energy of the falling object?

Answer 1

Answer and Explanation: Kinetic energy is related to movement: it is the energy an object possesses during the movement. it is calculated as:

`K=(1)/(2)mv^(2)`

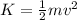
For the object thrown in the air:

`K=(1)/(2).2.[v(t)]^(2)`

`K=(-9.8t+24)^(2)`

`K=96.04t^(2)-470.4t+576`

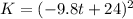
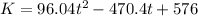
Kinetic energy of the object as a function of time:
`K=96.04t^(2)-470.4t+576`

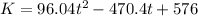
Potential energy is the energy an object possesses due to its position in relation to other objects. It is calculated as:

`U=mgh`

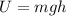
For the object thrown in the air:

`U=9.8.2.h(t)`

`U=9.8.2.(-4.9t^(2)+24t+60)`

`U=-96.04t^(2)+470.4t+1176`

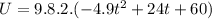
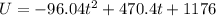
Potential energy as function of time:
`U=-96.04t^(2)+470.4t+1176`

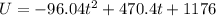
Total kinetic and potential energy, also known as mechanical energy is

TME =
`96.04t^(2)-470.4t+576` + (
`-96.04t^(2)+470.4t+1176`)

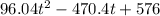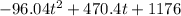TME = 1752

The expression shows that total energy of an object thrown in the air is constant and independent of time.