Question

A 237g sample of molybdnum metal is heated to 100.1 0C and then dropped into an insulated cup containing 244 g of water at 10.0 0C. If the final temperature of the water and metal in the cup is 15.3 0C, then what is the specific heat of molybdenum?

Answer 1

The specific heat of molybdenum is 0.254 joules per gram-Celsius.

Step-by-step explanation:

We consider the system formed by the molybdenum metal and water as our system, a control mass inside an insulated cup, that is, a container that avoids any energy and mass interactions between system and surroundings.

From statement we notice that metal is cooled down whereas water is heated. According to the First Law of Thermodynamics, we know that:

`Q_(metal) - Q_(water) = 0`

`Q_(metal) = Q_(water)`

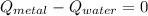
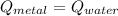
Where:

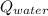`Q_(water)` - Heat received by water, measured in joules.

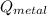`Q_(metal)` - Heat released by metal, measured in joules.

Now we expand this identity by definition of sensible heat:

`m_(metal)\cdot c_(metal)\cdot (T_(m,o)-T) = m_(water)\cdot c_(water)\cdot (T-T_(w,o))`

The specific heat of the metal is cleared within equation above:

`c_(metal) = (m_(water)\cdot c_(water)\cdot (T-T_(w,o)))/(m_(metal)\cdot (T_(m,o)-T))`

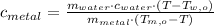
If we know that
`m_(water) = 0.237\,kg`,
`m_(metal) = 0.244\,kg`,
`c_(water) = 4186\,(J)/(kg\cdot ^(\circ)C)`,
`T_(w,o) = 10\,^(\circ)C`,
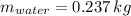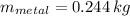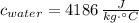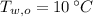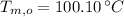`T_(m,o) = 100.10\,^(\circ)C` and
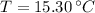`T = 15.30\,^(\circ)C`, the specific heat of molybdenum is:

`c_(metal) = ((0.237\,kg)\cdot \left(4186\,(J)/(kg\cdot ^(\circ)C) \right)\cdot (15.30\,^(\circ)C-10\,^(\circ)C))/((0.244\,kg)\cdot (100.10\,^(\circ)C-15.30\,^(\circ)C))`

`c_(metal) = 254.119\,(J)/(kg\cdot ^(\circ)C)`

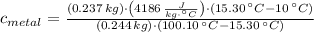
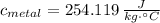
The specific heat of molybdenum is 0.254 joules per gram-Celsius.