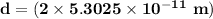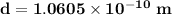Question

Practice entering numbers that include a power of 10 by entering the diameter of a hydrogen atom in its ground state, dH=1.06×10−10m d H = 1.06 × 10 − 10 m , into the answer box.

Answer 1

The diameter of the hydrogen
`\mathbf{d =1.0605 * 10^(-10)\ m}`

Step-by-step explanation:

From the given information:

Using the concept of Bohr's Model, the equation for the angular momentum can be expressed as:

`L = (nh)/(2 \pi)`

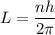
Where the generic expression for angular momentum is:

L = mvr.

replacing the value of L into the previous equation, we have:

`mvr= (nh)/(2 \pi)`

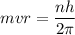
`v= (nh)/(2 \pi mr)` ----- (1)

The electron in the hydrogen atom posses an electrostatic force which gives a centripetal force.

`(ke^2)/(r^2) = (mv^2)/(r)` ----- (2)

replacing the value of v in equation (1) into (2), and taking r as the subject of the formula, we have:

`(ke^2)/(r) = m ((nh)/(2 \pi mr))^2`

`ke^2=(n^2h^2)/(4 \pi^2 mr)`

`r =(n^2h^2)/(4 \pi^2 mke^2)`

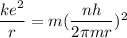
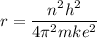
For ground-state n = 1

`h = (6.625 * 10^(-34) \ J.s)^2`

`m =( 9.1 * 10^(-31) \ kg)(9 * 10^9 \ N .m^2/C^2)`

`Ke = (1.6 * 10^(-19) \ C)^2`

`r =((1)^2(6.625 * 10^(-34))^2)/(4 \pi^2 (9.1 * 10^(-31) )(9 * 10^9 ) (1.6 * 10^(-19))^2)`

`r =(4.3890625 * 10^(-67))/(8.27720295 * 10^(-57))`

`\mathbf{r = 5.3025 * 10^(-11) \ m}`

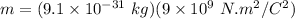
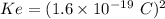
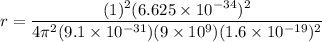
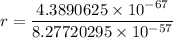
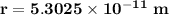
Therefore, the diameter of hydrogen d = 2r

`\mathbf{d = ( 2 * 5.3025 * 10^(-11) \ m})}`

`\mathbf{d =1.0605 * 10^(-10)\ m}}`