Given :
Capacitor , C = 55 μF .
Energy is given by :
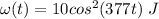 .
.
To Find :
The current through the capacitor.
Solution :
Energy in capacitor is given by :
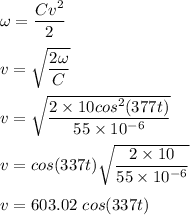
Now , current i is given by :
![i=C(dv)/(dt)\\\\i=C(d[603.02cos(337t)])/(dt)\\\\i=-55* 10^(-6)* 603.03* 337* sin(337t)\\\\i=-11.18\ sin(337t)](https://img.qammunity.org/2021/formulas/engineering/college/3h3vy9d51nvg983tmksq7z1r1m5c9bhxsu.png)
( differentiation of cos x is - sin x )
Therefore , the current through the capacitor is -11.18 sin ( 377t).
Hence , this is the required solution .