Answer:
145 kernels
Explanation:
The dimensions of the box are L= 5cm W=2.5cm H= 2.5.
Size of a kernal is 0.6 cm
We need to find number of kernels that could fit inside of the box. Let n be such kernals. So,
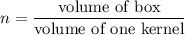
Kernal is in the shape of cube
So,
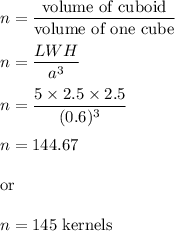
Hence, 145 kernels could fit inside of the box.