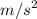Question

In April 1974, Steve Prefontaine completed a 10.0 km10.0 km race in a time of 27 min27 min , 43.6 s43.6 s . Suppose "Pre" was at the 7.85 km7.85 km mark at a time of 25.0 min25.0 min . If he accelerated for 60 s60 s and then maintained his increased speed for the remainder of the race, calculate his acceleration over the 60 s60 s interval. Assume his instantaneous speed at the 7.85 km7.85 km mark was the same as his overall average speed up to that time.

Answer 1

a = 0.161
`$m/s^2$`

Step-by-step explanation:

Given :

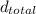`$ d_(total)` = 10 km = 10000 m

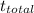`$t_(total) $` = 27 min 43.6 s

= 1663.6 s

`$d_1$` = 7.85 km = 7850 m

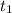`$t_1$` = 25 min = 1500 s

`$t_2$` = 60 s

Now the initial speed for the distance of 7.85 km is

`$ v_1 = (d_1)/(t_1) = (7850)/(1500)$` = 5.23 m/s

The velocity after 60 s after the distance of 7.85 kn is

`$v_2 = v_1 + at_2$`

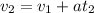
= 5.23 + a(60)

The distance traveled for 60 s after the distance of 7.85 km is

`$d_2 = v_1t_2+(1)/(2)at_2^2$`

`$d_2 = (5.23)(60)+(1)/(2)a(60)^2$`

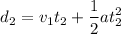
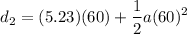
= 313.8 + a(1800)

The time taken for the last journey where the speed is again uniform is

`$t_3 = t_(total)-t_1-t_2 $`

= 1663.6 - 1500 - 60

= 103.6 s

Therefore, the distance traveled for the time
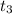`$t_3$` is

`$ d_3 = v_2 t_3$`

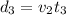
= (5.23+60a)(103.6)

= 541.8 + 6216 a

The total distance traveled,

`$ d_(total)= d_1 + d_2 + d_3$`

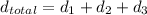
Now substituting the values in the above equation for the acceleration a is

10000 = 7850 + (313.6 + 1800a) + (541.8 + 6216a)

10000 = 8706.5 + 8016a

1294.4 = 8016a

a = 0.161
`$m/s^2$`