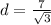Answer:
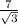
Explanation:
The shortest distance d, of a point (a, b, c) from a plane mx + ny + tz = r is given by:
 --------------------(i)
--------------------(i)
From the question,
the point is (5, 0, -6)
the plane is x + y + z = 6
Therefore,
a = 5
b = 0
c = -6
m = 1
n = 1
t = 1
r = 6
Substitute these values into equation (i) as follows;

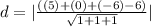
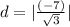
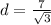
Therefore, the shortest distance from the point to the plane is