Question

A partial sum of an arithmetic sequence is given. Find the sum.

14 (3 + 0.26k) k = 0

Answer 1

72.3

Explanation:

Given that:

The arithmetic sequence:

`\sum \limits ^(14)_(k=0) (3 + 0.26k)`

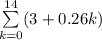
The first term of the sequence
`a_0` = 3 since k = 0

i.e (3 + 0.26(0)) = 3

The last term of the sequence
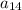`a_(14)` = 6.64

i.e (3+ 0.26(14)

= (3 + 3.64)

= 6.64

Total no of terms = 15 i.e from 0 to 14

∴

The partial sum of the arithmetic sequence =
`(Total \ no \ of \ terms )/(2) * (a_o+a_(15))}`

`=(15 )/(2) * (3+6.64)}`

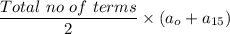
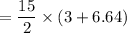
= 72.3