Question

. (a) Prove or disprove carefully and in detail: (i) Θ is transitive and (ii) ω is transitive. (b) Assume n is a positive integer. Algorithm A(n: int) int z = 0; int temp = 0; for (int i = 0; i < n ; i++) { for (int j = 0 ; j < i ; j++) { int temp = i + j ; int z = z + temp; } } System.out.println(z) ; What is the input size for Algorithm A? Analyze carefully and explicitly the time complexity of A in terms of the input size. Show all steps. Is A a polynomial time algorithm? Justify your answer.

Answer 1

The Following are the solution to this question:

Step-by-step explanation:

In Option a:

In the point (i)
`\Omega` is transitive, which means it converts one action to others object because if
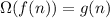`\Omega(f(n))=g(n)` indicates
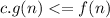`c.g(n)<=f(n)`. It's true by definition, that becomes valid. But if
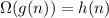`\Omega(g(n))=h(n)`, which implies
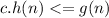`c.h(n)<=g(n)`. it's a very essential component. If
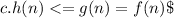`c.h(n) < = g(n) = f(n) \`. They
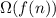`\Omega(f(n))` will also be
`h(n)`.

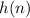In point (ii), The value of
`\Theta` is convergent since the
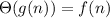`\Theta(g(n))=f(n)`. It means they should be dual a and b constant variable, therefore
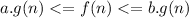`a.g(n)<=f(n)<=b.g(n)` could only be valid for the constant variable, that is
`(1)/(a)\ \ and\ \ (1)/(b)`.

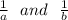In Option b:

In this algorithm, the input size value is equal to 1 object, and the value of A is a polynomial-time complexity, which is similar to its outcome that is
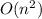`O(n^(2))`. It is the outside there will be a loop(i) for n iterations, that is also encoded inside it, the for loop(j), which would be a loop
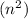`(n^(2))`. All internal loops operate on a total number of
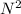`N^(2)` generations and therefore the final time complexity is
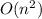`O(n^(2))`.