Answer:
the new height of the triangle = 2.449
Explanation:
Given that:
the sides of the triangle are 4m in length i.e they are equal. It shows that the triangle is known to be an equilateral triangle.
Let say the triangle is a triangle IJK
Let the length of the side to be i = 4
Definitely
IJ = JK = IK = i = 4
If a midline is drawn and cuts the equilateral triangle in two equal halves of a right-angle triangle. Then, suppose the midline is L
Then ;

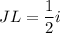
Let consider triangle IJL
(IL)² = (IJ)² - (JL)²

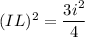
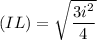
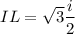
Area of triangle IJK can be expressed as:
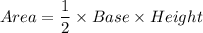
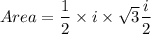
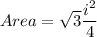
where, i = 4
Then:
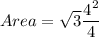
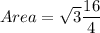
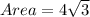
when the area is exactly half of the original triangle's area, the new height is :

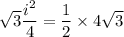

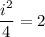
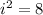
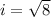
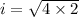
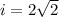
Finally, the new height of the new triangle is:
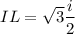
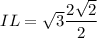
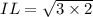
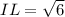
IL = 2.449 m