Question

When 229.0 J of energy is supplied as heat to 3.00 mol of Ar(g) at constant pressure the temperature of the sample increases by 2.55 K. Assuming that in the experiment the gas behaves as an ideal gas, calculate the molar heat capacities at constant volume and at constant pressure of Ar(g).

Answer 1

The molar heat capacity at constant volume is 21.62 JK⁻¹mol⁻¹

The molar heat capacity at constant pressure is 29.93 JK⁻¹mol⁻¹

Step-by-step explanation:

We can calculate the molar heat capacity at constant pressure from

`C_(p,m) = (C_(p) )/(n)`

Where
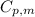`C_(p,m)` is the molar heat capacity at constant pressure

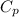`{C_(p) }` is the heat capacity at constant pressure

and
`n` is the number of moles

Also
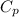`{C_(p) }` is given by

`{C_(p) } = (\Delta H)/(\Delta T)`

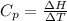
Hence,

`C_(p,m) = (C_(p) )/(n)` becomes

`C_(p,m) = (\Delta H )/(n \Delta T)`

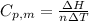
From the question,

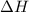`\Delta H` = 229.0 J

`n` = 3.00 mol

`\Delta T` = 2.55 K

Hence,

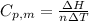`C_(p,m) = (\Delta H )/(n \Delta T)` becomes

`C_(p,m) = (229.0)/((3.00) (2.55))`

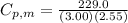
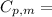`C_(p,m) =` 29.93 JK⁻¹mol⁻¹

This is the molar heat capacity at constant pressure

For, the molar heat capacity at constant volume,

From the formula

`C_(p,m) = C_(v,m) + R`

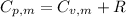
Where
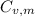`C_(v,m)` is the molar heat capacity at constant volume

and
`R` is the gas constant (
`R` = 8.314 JK⁻¹mol⁻¹)

Then,

`C_(v,m) = C_(p,m) - R`

`C_(v,m) = 29.93 - 8.314`

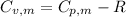
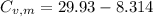
`C_(v,m) =` 21.62 JK⁻¹mol⁻¹

This is the molar heat capacity at constant volume