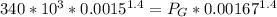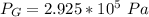Answer:
The value is
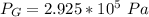
Step-by-step explanation:
From the question we are told that
The volume of the bottle is
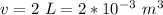
The gauge pressure of the air is
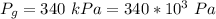
Generally the volume of air before the bottle is turned upside down is
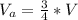
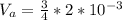

Generally the volume air when the bottle is turned upside-down is
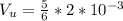
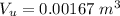
From the the mathematical relation of adiabatic process we have that
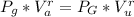
Here r is a constant with a value r = 1.4
So