Answer:
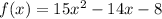
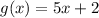
Explanation:
Represent the two polynomials with f(x) and g(x)
The question requires that we assume values for f(x) and g(x) as long as the condition in the question is met;
Let
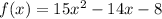
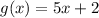
To determine if the condition is met, we need to divide f(x) by g(x)
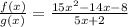
Factorize the numerator
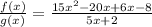

Cross out 5x + 2
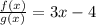
The result is referred to as quotient, Q
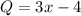
Note that Q and g(x) have the same degree of 1