Answer:
The final temperature is
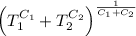
and the maximum amount of workdone is
 .
.
Step-by-step explanation:
Assume that
 is the reservior having temperature
is the reservior having temperature
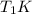 and heat capicity
and heat capicity
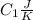 and
and
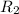 is the reservior having temperature
is the reservior having temperature
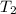 and heat capicity
and heat capicity
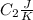 .
.
The work will be extracted till that both the reservior reach the thermal equilibrium. Let the final temperature of both the reservior is
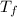 .
.
Let total
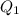 heat is extracted by the heat engine from the reservior
heat is extracted by the heat engine from the reservior
 and its temperature decreases from
and its temperature decreases from
 to
to
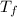 and
and
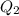 heat is rejected by the heat engine to the reservior
heat is rejected by the heat engine to the reservior
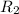 and its temperature decreases from
and its temperature decreases from
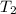 to
to
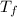 .
.
So, The maximum amount of work done,
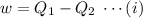
Now, as the heat engine is reversible, so change is entropy for the universe is 0, which means sum of change in entropy for the ststem as well as surrounding is 0.
As shown in figure, the system is the reversible engine, so, change is entropy for the system is 0. Hence, change in entropy for the the surrounding is 0.
As temperature of
 is changing fron
is changing fron
 to
to
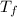 , so, change in entropy of surrounding due to transfer of
, so, change in entropy of surrounding due to transfer of
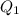 is
is
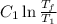 .
.
Similarly, change in entropy of surrounding due to transfer of
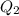 is
is
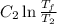 .
.
As the net change in entropy of the surrounding is 0.
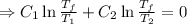
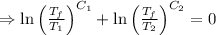
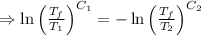
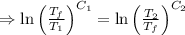
 [taking anti-log both the sides]
[taking anti-log both the sides]

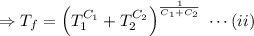
This is the required final temperature.
Now, from equarion (i), the maximum amount of work done is

As
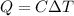
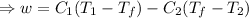
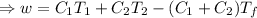
From equation
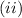 ,
,
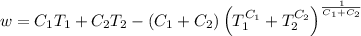
This is the required maximum workdone.