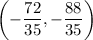Question

Solve the system of linear equations. Give your solution as an ordered pair, either as a fraction or a decimal with at least 3 decimal places.

1/8x - 1/2y = 1
1/3x + 1/8y = -1

Answer 1

`\left(-(72)/(35),-(88)/(35)\right)`

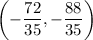
Explanation:

`\textsf{Equation 1}: \quad (1)/(8)x-(1)/(2)y=1`

`\textsf{Equation 2}: \quad (1)/(3)x+(1)/(8)y=-1`

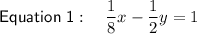
Multiply Equation 1 by 8:

`\textsf{Equation 1}: \quad 8\left((1)/(8)x-(1)/(2)y=1\right)\implies x-4y=8`

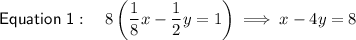
Multiply Equation 2 by 32:

`\textsf{Equation 2}: \quad 32\left((1)/(3)x+(1)/(8)y=-1\right)\implies (32)/(3)x+4y=-32`

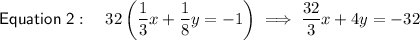
Add the new equations together to eliminate y:

`\begin{array}{ l r c r c r}& x & - & 4y & = & 8\\\\+ & (32)/(3)x & + & 4y & = & -32\\\\\cline{1-6}\\& (35)/(3)x & & & = & -24\end{array}`

`\implies (35)/(3)x=-24`

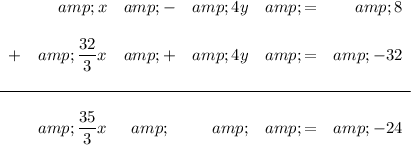
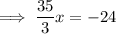
Multiply both sides by 3:

`\implies 35x=-72`

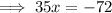
Divide both sides by 35:

`\implies x=-(72)/(35)`

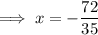
To find the y-value, substitute the found value of x into Equation 1 and solve for y:

`\implies (1)/(8)\left(-(72)/(35)\right)-(1)/(2)y=1`

`\implies -(72)/(280)-1=(1)/(2)y`

`\implies -(44)/(35)=(1)/(2)y`

`\implies y=-(88)/(35)`

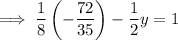
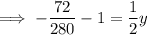
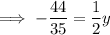
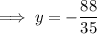
Solution

`\left(-(72)/(35),-(88)/(35)\right)`