Answer:
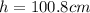
Step-by-step explanation:
Hello,
In this case, considering the density and mass of both water and heptane we first compute the volume of each one:
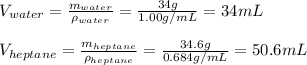
Now, the total volume is:
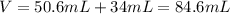
Which is equal to:
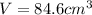
Then, by knowing that the volume of a cylinder is πr²h or π(D/2)²h, we solve for the height as follows:
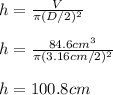
Best regards.