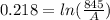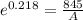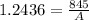Question

The next two questions provide some more practice on calculations using half-lives. The isotope 64Cu has t1/2 of 12.7 hours. If the initial concentration of this isotope in an aqueous solution is 845 ppm, what will the abundance be after 4.00 hours? To solve this problem, first use equation (7) to determine k for 64Cu; then use this k value in equation (6) to obtain the amount of 64Cu, A, remaining after 4.00 hours if the amount present at the start, A0, is 845 ppm.

Answer 1

The value is
`A = 679.5 \ ppm`

Step-by-step explanation:

From the question we are told that

The half life of
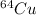`^(64)Cu` is
`t_h = 12.7 \ hr`

The initial concentration is
`A_o  = 845 \  ppm`

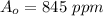
The time duration is
`t =  4 \  hr`

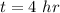
Generally the rate constant is mathematically represented as

`k =  (0.693)/(t_h)`

`k =  (0.693)/(12.7)`

`k = 0.0545 \  hr^(-1)`

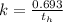
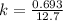
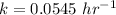
This rate constant is also mathematically represented as

`k =  (1)/(t) *  ln ((A_o)/(A))`

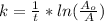
Here A is the remaining concentration after t

So

`0.0545 =  (1)/(4) *  ln ((845)/(A))`

`0.218 =  ln ((845)/(A))`

`e^(0.218) =   (845)/(A)`

`1.2436 =   (845)/(A)`

`A =   (845)/(1.2436)`

`A =   679.5 \  ppm`