Answer:
The average velocity of the particle on the time interval is -2 meters per second.
Explanation:
Let be
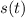 the position curve which is continuous on the time interval
the position curve which is continuous on the time interval
![[a,b]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/dyyh30s5r4ox0wg76shisxuulr9zptlacg.png) . The average velocity (
. The average velocity (
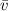 ), measured in meters per second, on the time interval is represented by the following expression:
), measured in meters per second, on the time interval is represented by the following expression:
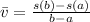
Where:
 ,
,
 - Initial and final times, measured in seconds.
- Initial and final times, measured in seconds.
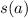 ,
,
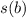 - Initial and final positions, measured in meters.
- Initial and final positions, measured in meters.
If we know that
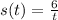 ,
,
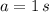 and
and
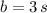 , the average velocity of the particle on the time interval is:
, the average velocity of the particle on the time interval is:
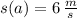
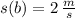
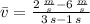

The average velocity of the particle on the time interval is -2 meters per second.