Question

The power generated by an electrical circuit (in watts) as a function of its current x (in amperes) is modeled by: P(x)=-12x^2+120x What current will produce the maximum power?

Answer 1

Answer: 5

Explanation:

khan

Answer 2

A current of 5 amperes will produce the maximum power.

Explanation:

Let be
`p(x) = -12\cdot x^(2)+120\cdot x`, where
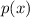`p(x)` is measured in watts and
`x` in amperes. At first we must obtain the first and second derivatives of the function to determine the current associated with maximum power. That is:

First derivative

`p'(x) = -24\cdot x + 120`

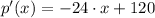
Second derivative

`p''(x) = -24\cdot x`

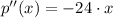
Now, we equalize the first derivative to zero and solve it afterwards: (First Derivative Test)

`-24\cdot x + 120 = 0`

`x = 5\,A`

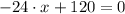
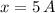
The only critical point is
`x = 5\,A`.

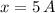As next step we need to assure that critical point leads to an absolute maximum by evaluating the critical point found above in the second derivative: (Second Derivative Test)

`p(5)'' = -24\cdot (5)`

`p''(5) = -120`

Which indicates that critical point leads to an absolute maximum.

A current of 5 amperes will produce the maximum power.