Question

☆☆PLEASE HELP ASAP!!☆☆

Add one term to the polynomial expression 14x^19 – 9x^15 + 11x^4 + 5x^2 + 3 to make it into a 22nd degree polynomial.​

Answer 1

The new expression is
`p' = 5\cdot x^(2)+11\cdot x^(4)-9\cdot x^(15)+14\cdot x^(19)+12\cdot x^(22)`.

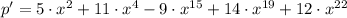Explanation:

A polynomial is a sum of algebraic monomials such that:

`p = \Sigma_(i=0)^(n) c_(i)\cdot x^(i)`

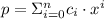
Where
`n` is the degree of the polynomial and
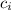`c_(i)` is the i-th coefficient of the polynomial. A 22nd degree polynomial has
`n = 22`, so that given polynomial must added by a monomial with grade 22. Thus:

If
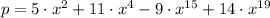`p = 5\cdot x^(2) + 11\cdot x^(4)-9\cdot x^(15)+14\cdot x^(19)` and
`q = 12\cdot x^(22)`, then we have:

`p' = p+q`

`p' = 5\cdot x^(2)+11\cdot x^(4)-9\cdot x^(15)+14\cdot x^(19)+12\cdot x^(22)`

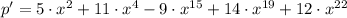
The new expression is
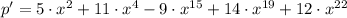`p' = 5\cdot x^(2)+11\cdot x^(4)-9\cdot x^(15)+14\cdot x^(19)+12\cdot x^(22)`.