Answer:
h(x)=1/4x
Explanation:
To find the inverse of a function, switch the "x" and the "y". The f(x) can be considered as "y".

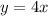
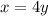
We want to isolate y. 4 and y are being multiplied. The inverse of multiplication is division. Divide both sides of the equation by 4.
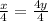
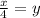
x/4 can be rewritten as 1/4x.
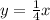

The inverse of the function f(x)=4x is h(x)=1/4x