Question

The interval for which the quotient is continuous is the intersection of the above intervals. therefore, the quotient 12 x 12 x is continuous on the interval

Answer 1

The common continuous interval will be (0,∞).

Explanation:

Given that,

The numerator = 12+√x

The denominator = √12+x

We know that,

For the numerator,

Any function under square root should be greater than and equal to the zero.

`x\geq 0`

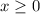
So, the continuous interval is (0, ∞)

For the denominator,

`√(12+x)>0`

`12+x>0`

`x>-12`

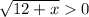
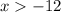
The interval for the continuous and non zero function is,

(-12, ∞)

We need to calculate the continuous interval

Using given quotient

`(12+√(x))/(√(12+x))`

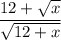
The continuous interval of numerator and denominator are (0, ∞) and (-12, ∞).

Hence, The common continuous interval will be (0,∞).