Answer:
Rule : Vertical line test, unique output for each input, mapping should one-one and onto, each x-value has unique y-value.
Exception : Inverse trigonometric functions
Explanation:
A relation is a function if there exist a unique output for each input value.
We use vertical line test to check whether the graph intersect a vertical line at most once or not. If it intersect the graph more than once than it is not a function.
In table, first we identify the input and output variable, then we check there exist a unique output for each input value.
In map diagram, we check each element in the domain must be matched with exactly one element in the range, i.e., one-one and onto, then it is called function.
Set of ordered pairs, we check that each x-value has unique y-value.
Exception to the rule : Inverse trigonometric functions are not real valued functions, so these are the exceptions.
For example :
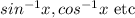 .
.