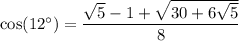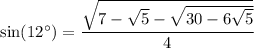1 Answer

Praveen Ramalingam · Answer 1 · 2021-10-13T22:10:47+0000

But z is already given in rectangular form... A complex number in rectangular form looks like
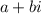a+bi , where
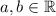$a,b\in\mathbb{R}$ .

Perhaps you're supposed to write cos(12º) and sin(12º) in non-trigonometric form? In that case, we want exact forms of these numbers.

Note that 12º = 60º/5. Consider the identities

$\cos(5t)=\cos^5t-10\sin^2t\cos^3t+5\sin^4t\cos t$

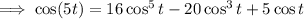
$\implies\cos(5t)=16\cos^5t-20\cos^3t+5\cos t$

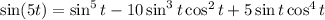
$\sin(5t)=\sin^5t-10\sin^3t\cos^2t+5\sin t\cos^4t$

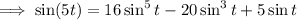
$\implies\sin(5t)=16\sin^5t-20\sin^3t+5\sin t$

(both of which follow from DeMoivre's theorem)

We have
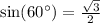$\sin(60^\circ)=\frac{\sqrt3}2$ and
$\cos(60^\circ)=\frac12$ , so we get

$\cos(12^\circ)=\frac{\sqrt5-1+√(30+6\sqrt5)}8$

$\sin(12^\circ)=\frac{\sqrt{7-\sqrt5-√(30-6\sqrt5)}}4$

Please log in or register to add a comment.