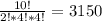Question

How many distinct ways are there to arrange 2 pink marbles, 4 blue marbles, and 4 orange marbles in a row?

Answer 1

3150 different ways to rearrange the marbles.

Explanation:

This is a very simple combinatoric. The formula for a situation in which we are looking to find the distinct ways of arrangement for three different objects is:

`(n!)/(a*b*c)`

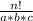
where n represents the total number of objects to rearrange.

a,b,c represents the the total ways to move around the their corresponding type of object in a similiar fashion. (i.e., a = (# of pink marbles)!, b = (# blue marbles)!, c = (# of orange marbles)!).

Since there is always a x! amount of ways to rearrange a collection of similiar order, we can account for the overcounting via taking the factorial of each of the different quantities.

Thus, we get

`(10!)/(2!*4!*4!) = 3150`