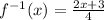Answer:
The inverse of f(x) is
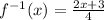
Explanation:
Explanation:-
Given
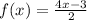
Inverse of f(x)
f(x) is a one-one function
let f(x₁) and f(x₂) be two functions are
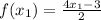
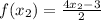
⇒
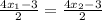
⇒ 4 x₁ - 3 = 4 x₂ - 3
⇒ 4 x₁ = 4 x₂
⇒ x₁ = x₂
Given function is one-one function
y = f(x) =
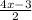
⇒ 2 y = 4 x - 3
⇒ 4 x = 2 y + 3
⇒
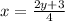
⇒ f⁻¹(x)
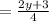
Given function f(x) is onto function
Therefore f(x) is one-one and onto function