Answer:
We have to solve each inequality separately and write the word "or" in between them. We can write union between the solution sets of both inequalities.
Explanation:
OR-type inequalities : In these types of inequalities we have to solve each inequality separately and write the word "or" in between them. The final answer is the union of solution of each inequality.
For example:
Let OR-type inequalities are
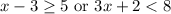
On solving these inequities separately, we get
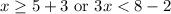
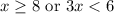
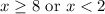
It means the value of is either less than 2 or greater than or equal to 8. 2 is not included in the solution set.

Therefore, the we have to solve each inequality separately and write the word "or" in between them. We can write union between the solution sets of both inequalities.