Answer:
There are 199 pairs of consecutive natural numbers whose product is less than 40000.
Explanation:
We notice that such statement can be translated into this inequation:
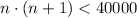
Now we solve this inequation to the highest value of
 that satisfy the inequation:
that satisfy the inequation:
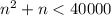
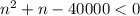
The Quadratic Formula shows that roots are:
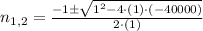
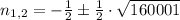

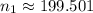
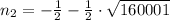
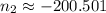
Only the first root is valid source to determine the highest possible value of
 , which is
, which is
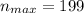 . Each natural number represents an element itself and each pair represents an element as a function of the lowest consecutive natural number. Hence, there are 199 pairs of consecutive natural numbers whose product is less than 40000.
. Each natural number represents an element itself and each pair represents an element as a function of the lowest consecutive natural number. Hence, there are 199 pairs of consecutive natural numbers whose product is less than 40000.