Answer:

Explanation:
Given, the length of the rectangular dog run is 18 feet.
Formula: Perimeter = 2 ( length + width)
Let width be x.
Then, Perimeter = 2 (18 + x ) feet
The perimeter of the dog run must be at least 42 feet and no more than 72 feet.
That is
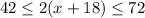
Divide inequality by 2, we get

Subtract 18 from each side, we get

Required inequality :
