Question

pasar las siguientes frecuencias medidas en r.p.m a sg∧-1 .830 r.p.m .4500 r.p.m .720 r.p.m .3832 r.p.m URGENTE PORFAVOR¡¡¡¡¡

Answer 1

The frequencies are 13.8 Hz, 75 Hz, 12 Hz and 63.8 Hz.

Step-by-step explanation:

Given that,

The frequency in r.p.m

`f_(1)=830\ rpm`

`f_(2)=4500\ r.p.m`

`f_(3)=720\ r.p.m`

`f_(4)=3832\ r.p.m`

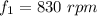
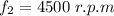
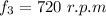
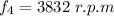
Suppose, we find the frequency in hz.

We know that,

One r.p.m is equal to the one divided by 60 Hz.

`1\ r.p.m=(1)/(60)\ Hz`

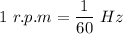
We need to calculate the frequency in Hz

Using formula for frequency in Hz

For f₁,

`f_(1)=830\ r.p.m`

`f_(1)=(830)/(60)\ Hz`

`f_(1)=13.8\ Hz`

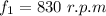
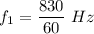
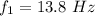
For f₂,

`f_(2)=4500\ r.p.m`

`f_(2)=(4500)/(60)\ hz`

`f_(2)=75\ Hz`

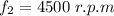
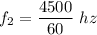
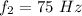
For f₃,

`f_(3)=720\ r.p.m`

`f_(3)=(720)/(60)\ hz`

`f_(3)=12\ Hz`

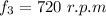
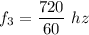
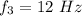
For f₄,

`f_(4)=3832\ r.p.m`

`f_(4)=(3832)/(60)\ hz`

`f_(4)=63.8\ Hz`

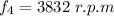
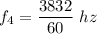
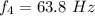
Hence, The frequencies are 13.8 Hz, 75 Hz, 12 Hz and 63.8 Hz.