Question

Please prove this........​

Answer 1

Answer: see proof below

Explanation:

Given: A + B + C = π → C = π - (A + B)

→ sin C = sin(π - (A + B)) cos C = sin(π - (A + B))

→ sin C = sin (A + B) cos C = - cos(A + B)

Use the following Sum to Product Identity:

sin A + sin B = 2 cos[(A + B)/2] · sin [(A - B)/2]

cos A + cos B = 2 cos[(A + B)/2] · cos [(A - B)/2]

Use the following Double Angle Identity:

sin 2A = 2 sin A · cos A

Proof LHS → RHS

LHS: (sin 2A + sin 2B) + sin 2C

`\text{Sum to Product:}\qquad 2\sin\bigg((2A+2B)/(2)\bigg)\cdot \cos \bigg((2A - 2B)/(2)\bigg)-\sin 2C`

`\text{Double Angle:}\qquad 2\sin\bigg((2A+2B)/(2)\bigg)\cdot \cos \bigg((2A - 2B)/(2)\bigg)-2\sin C\cdot \cos C`

`\text{Simplify:}\qquad \qquad 2\sin (A + B)\cdot \cos (A - B)-2\sin C\cdot \cos C`

`\text{Given:}\qquad \qquad \quad 2\sin C\cdot \cos (A - B)+2\sin C\cdot \cos (A+B)`

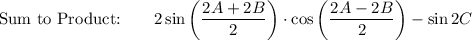
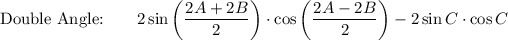
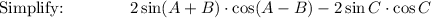
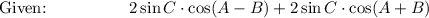
`\text{Factor:}\qquad \qquad \qquad 2\sin C\cdot [\cos (A-B)+\cos (A+B)]`

`\text{Sum to Product:}\qquad 2\sin C\cdot 2\cos A\cdot \cos B`

`\text{Simplify:}\qquad \qquad 4\cos A\cdot \cos B \cdot \sin C`

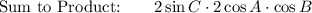
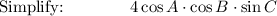
LHS = RHS: 4 cos A · cos B · sin C = 4 cos A · cos B · sin C
`\checkmark`