Answer:
1)
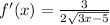
2)
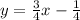
Explanation:
So we have the function:
1)
And we want to find its derivative using the limit definition:

So, let's do so:
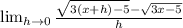
Simplify the first square root:
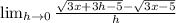
Now, let's remove the square root by multiplying by its conjugate. So:
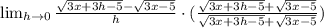
In the numerator, difference of two squares. In the denominator, multiply:
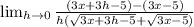
Distribute the numerator:
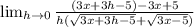
Simplify:
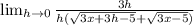
Cancel out the h:

Direct substitution:
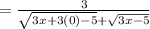
Simplify:

Combine like terms:
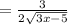
Therefore:
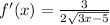
Your answer is indeed correct!
2)
Now, let's find the equation of the tangent line to the graph at x=3.
Remember what the derivative gives us. The derivative tells us the slope of the tangent line to a graph at a certain point. So, let's substitute 3 into f'(x) to find the slope of our tangent line:

Multiply and subtract:
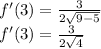
Simplify:
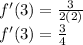
Therefore, the slope of our tangent line is 3/4.
Now, let's find the equation of the line using the point-slope form. So, we need to point at x=3 of the original graph. So, substitute 3 into the original function:
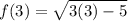
Multiply, subtract, and simplify:
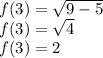
Therefore, our point is (3,2).
Now, we can use the point-slope form, where:

Let (3,2) be (x₁, y₁) and substitute 3/4 for m. Therefore:
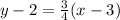
Distribute:
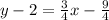
Add 2 to both sides:
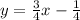
And we're done!