Answer:
61.5752159 units³
Explanation:
The height of a cone can be found using the following formula:
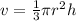
We know that the height is 14.7 and the radius is 2.
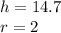
Substitute the values into the formula.
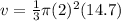
Evaluate the exponent.
⇒ 2²= 2*2 = 4
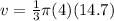
Multiply 4 and 14.7
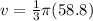
Multiply 1/3 and pi.
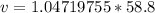
Multiply the two numbers together.
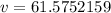
Add appropriate units. Volume is cubic units, and we aren't given units. So, we should use cubic units.
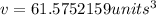
The volume of the cone is 61.5752159 cubic units.