Question

Solve the equation x=5/3 pi r ^3

A.
B
C
D?

Answer 1

How to solve?

Here, we just have to express r in terms of x when we are provided with the relation between x and r. We have to flip and sent it to the Right hand side.

Solution:

We have,

• 
  `\large{ \rm{x = (5)/(3) \pi {r}^(3) }}`

Solving it further,

`\large{ \longrightarrow{ \rm{x = (5)/(3) \pi {r}^(3) }}}`

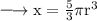
Taking 5/3 to the other side by dividing it,

`\large{ \longrightarrow{ \rm{ (3x)/(5) = \pi {r}^(3) }}}`

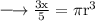
Now, taking π to the other side by dividing it,

`\large{ \longrightarrow{ \rm{ (3x)/(5\pi) = {r}^(3) }}}`

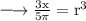
Cube rooting LHS to get r

`\large{ \longrightarrow{ \rm{ \sqrt[3]{ (3x)/(5\pi) } = r}}}`

Flipping it,

`\large{ \longrightarrow{ \rm{r = \sqrt[3]{ (3x)/(5\pi) } }}}`

So, the correct option:

`\huge{ \boxed{ \bf{ \red{Option \: B}}}}`

━━━━━━━━━━━━━━━━━━━━

Answer 2

B (3x / ( 5pi)) ^ 1/3 = r

Explanation:

x=5/3 pi r ^3

Multiply each side by 3/5

3/5 x= pi r ^3

Divide each side by pi

3x / ( 5pi) = pi r^3 /pi

3x / ( 5pi) = r^3

Take the cube root of each side

(3x / ( 5pi)) ^ 1/3 = r^3 ^ 1/3

(3x / ( 5pi)) ^ 1/3 = r